Birkhoff–Grothendieck theorem
In mathematics, the Birkhoff–Grothendieck theorem classifies holomorphic vector bundles over the complex projective line. In particular every holomorphic vector bundle over 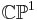 is a direct sum of holomorphic line bundles. The theorem was proved by Grothendieck (1957, Theorem 2.1), and is more or less equivalent to Birkhoff factorization introduced by Birkhoff (1909).
is a direct sum of holomorphic line bundles. The theorem was proved by Grothendieck (1957, Theorem 2.1), and is more or less equivalent to Birkhoff factorization introduced by Birkhoff (1909).
Contents |
Statement
More precisely, the statement of the theorem is as the following.
Every holomorphic vector bundle 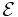 on
on 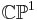 is holomorphically isomorphic to a direct sum of line bundles:
is holomorphically isomorphic to a direct sum of line bundles:
The notation implies each summand is a Serre twist some number of times of the trivial bundle. The representation is unique up to permuting factors.
Generalization
The same result holds in algebraic geometry for vector bundles over 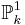 for
for  any field.
any field.
See also
References
- Birkhoff, George David (1909), "Singular points of ordinary linear differential equations", Transactions of the American Mathematical Society 10 (4): 436–470, ISSN 0002-9947, JFM 40.0352.02, JSTOR 1988594
- Grothendieck, Alexander (1957), "Sur la classification des fibres holomorphes sur la sphere de Riemann", American Journal of Mathematics 79: 121•138, doi:10.2307/2372388.
- Okonek, C.; Schneider, M.; Spindler, H. (1980), Vector bundles on complex projective spaces, Progress in Mathematics, Birkhäuser.
